The Fourier Transform is a mathematical operation that transforms a function of time (or space) into a function of frequency. It decomposes a complex signal into its constituent sinusoidal components, each with a specific frequency, amplitude, and phase. This is particularly useful in many fields, such as signal processing, physics, and engineering, because it allows for analysing the frequency characteristics of signals. The Fourier Transform provides a bridge between the time and frequency domains, enabling the analysis and manipulation of signals in more intuitive and computationally efficient ways. The result of applying a Fourier Transform is often represented as a spectrum, showing how much of each frequency is present in the original signal.
\[\Large\boxed{\boxed{\widehat{f}(\xi) = \int_{-\infty}^{\infty} f(x)\ e^{-i 2\pi \xi x}\,\mathrm dx, \quad \forall\xi \in \mathbb{R}.}}\]
Inverse Fourier Transform:
\[\Large\boxed{\boxed{ f(x) = \int_{-\infty}^{\infty} \widehat f(\xi)\ e^{i 2 \pi \xi x}\,\mathrm d\xi,\quad \forall x \in \mathbb R.}}\]
The equation allows us to listen to mp3s today. Digital Music Couldn’t Exist Without the Fourier Transform: http://bit.ly/22kbNfi
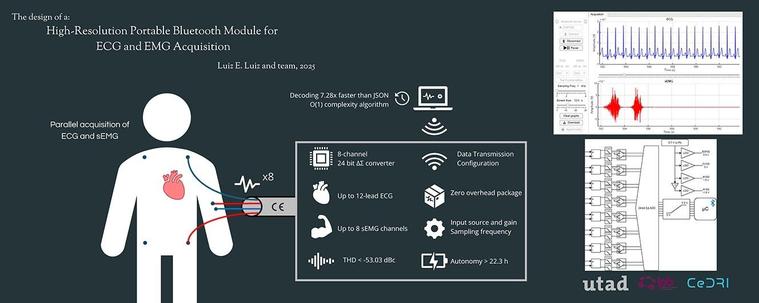
Can we push the boundaries of wearable biosignal monitoring for real-world clinical and research use?
High-resolution portable bluetooth module for ECG and EMG acquisition. Computational and Structural Biotechnology Journal, DOI: https://doi.org/10.1016/j.csbj.2025.04.020
CSBJ Smart Hospital: https://www.csbj.org/smarthospital